AI+Science Reading Group
I participate in a reading group about AI+Science. Its outline is as follows:
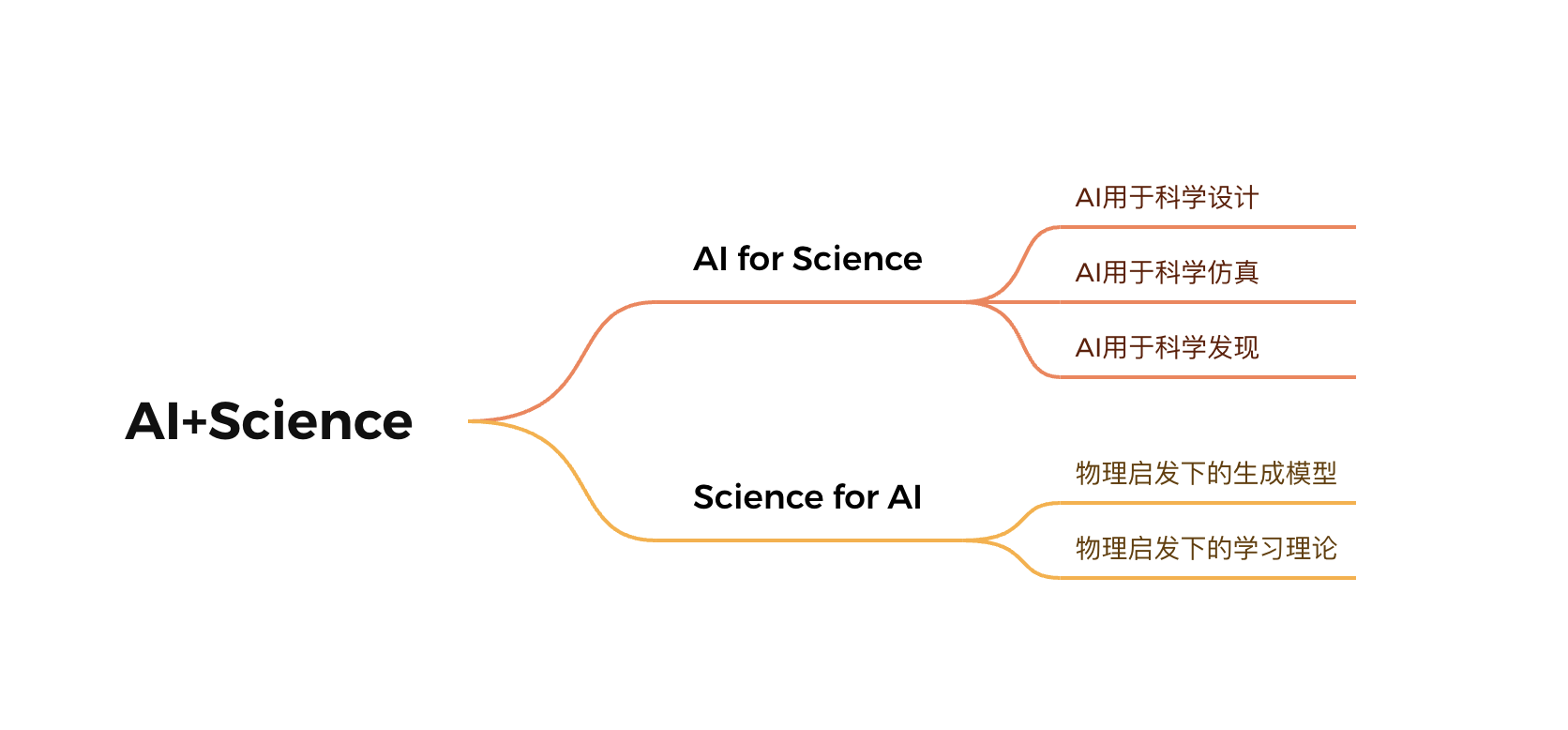
AI for Scientific Simulation
Tailin Wu identified key points as follows:
- Symmetry and conservation laws: How to design the architecture of machine learning models so that the symmetry and conservation laws of physical systems can be strictly obeyed?
- Multiscale and multiresolution: The spatiotemporal dynamics of many systems span multiple scales and resolutions, with certain parts being highly dynamic and requiring very fine resolution to accurately simulate, while other parts are relatively static. How to design the architecture of machine learning models that can achieve a reasonable balance between accuracy and computational complexity?
- Large-scale characteristics: When there are millions or even billions of degrees of freedom needed to simulate a system, how to design a model to reduce computational complexity, or make the architecture of machine learning adapt to such large-scale characteristics?
- Accuracy of long-term prediction: Many system simulations require the use of the same model to autoregressively predict several dozen or even thousands of steps. In this process, the prediction errors of the model will accumulate, causing the input of the machine learning model in autoregression to come from out-of-distribution. How to reduce the error of long-term prediction and improve its accuracy?
He also suggests to read the following papers with helpful comments:
-
GraphCast: Learning skillful medium-range global weather forecasting
DeepMind 提出的一个用图神经网络作为代理模型来实现中程天气天气预报(7天)。其模型超越了开发了几十年的传统方法天气预报的准确度。其使用的多尺度图神经网络架构和训练方法有借鉴意义。
-
Fourier Neural Operator for Parametric Partial Differential Equations
本文提出了基于傅里叶变换的神经算子(neural operator)架构,能够实现函数空间之间的直接映射。其在偏微分方程的模拟中具有很好的准确率,并且能够实现superresolution。
-
Learning Mesh-Based Simulation with Graph Networks
提出了MeshGraphNets,能够很好的进行基于网格的模拟(mesh-based simulation),能够用于流体力学,计算机图形学等物理仿真领域。
-
Learning Controllable Adaptive Simulation for Multi-resolution Physics
针对众多科学模拟中的多分辨率的问题,提出了一个新的方法,用一个MeshGraphNet学习系统的演化,另一个MeshGraphNet学习空间局域的再网格化(remeshing),实现准确率和计算量的合理权衡。
-
Highly accurate protein structure prediction with AlphaFold
提出了著名的AlphaFold 2.0,其对蛋白质三维构象的预测的准确度极大超越了其他方法。
-
Deep Potential Molecular Dynamics: A Scalable Model with the Accuracy of Quantum Mechanics
提出了Deep Potential Molecular Dynamics的方法用于分子模拟。其模型包含系统的所有自然对称性,其准确率达到了量子力学精度。
-
E(n) Equivariant Graph Neural Networks
提出了等变图神经网络,将空间平移和旋转的等变性(equivariance)植入到图神经网络的设计中,实现了在分子性质预测的优越性能。其将对称性植入神经网络的设计的思想值得学习。
E(n) Equivariant Graph Neural Networks.
It is equivariant to \(E(n)\) and permutations. This is achieved by forward propagating in the following way:
\[m_{ij} = \phi_{e}(h_{i}^{l},h_{j}^{l},\|x_{i}^{l}-x_{j}^{l}\|^2,a_{ij})\\ x_{i}^{l+1}=x_{i}^{l}+C\sum_{j\neq i}(x_{i}^{l}-x_{j}^{l})\phi_{x}(m_{ij})\\ m_{i}=\sum_{j\neq i}m_{ij}\\ h_{i}^{l+1}=\phi_{h}(h_{i}^{l}, m_i)\]The proof sketch is intuitive. At first, keep in mind that EGNN layer transforms a tuple \((h_{i}^{l},x_{i}^{l})\) into a tuple \((h_{i}^{l+1},x_{i}^{l+1})\). Suppose \(h_{i}^{l}\) has been invariant to \(E(n)\), which is definitely correct since such group elements act on \(x_{i}^{l}\) rather than \(h_{i}^{l}\). Then \(m_{ij}\) must be invariant to \(E(n)\) because
\[(Qx_{i}^{l}+g) - (Qx_{j}^{l}+g) = Q(x_{i}^{l}-x_{j}^{l})\]and \(Q\) is orthogonal matrix for expressing rotation operation so that the distance is preserved. Finally, \(m_{i}\) is invariant to \(E(n)\) as all \(m_{ij}\) are. Thus, \(h_{i}^{l+1}\) is invariant to \(E(n)\). Similarly, \(x_{j}^{l+1}\) is equivariant to \(E(n)\).
Inferring edges. When adjacency has not been given, considering a complete graph is OK but not scalable. To learn a function mapping \(m_{ij}\) to \(e_{ij} \in [0, 1]\) for weighting \(m_{ij},\forall j\) in aggregation.
Molecular dynamics simulation. To extend EGNN with momentum, namely, transforming \((h_{i}^{l},x_{i}^{l}, v_{i}^{l})\) to \((h_{i}^{l+1},x_{i}^{l+1}, v_{i}^{l+1})\). To this end, EGNN can make forward propagation in the following way:
\[v_{i}^{l+1}=\phi_{v}(h_{i}^{l})v_{i}^{\text{init}}+C\sum_{j\neq i}(x_{i}^{l}-x_{j}^{l})\phi_{x}(m_{ij})\\ x_{i}^{l+1}=x_{i}^{l}+v_{i}^{l+1}\]Note that $v$ stands for velocity, and thus when we say \(x_{i}^{l+1}\), in this case, is still equivariant to \(E(n)\), we mean that previoius \(x\) becomes \(Qx+g\) and initial \(v\) becomes \(Qv\) rather than \(Qv+g\).
Graph Autoencoder. There is a symmetry problem, that is, when there is no or identical attributes, i.e., same \(h_{i}^{0}\) for all nodes. In this case, there would be same node embeddings for all nodes, and thus same predicted probability of the existence of \(e_{ij}\). A convention to resolve this issue is to add Gaussian noise to \(h_{i}^{0}\).
Other related concepts and questions. What spherical harmonics is. What radial direction and radial field are. How to interpret the extension with momentum. What isometric invariant is.
Highly accurate protein structure prediction with AlphaFold
AI for Scientific Design
To be continued…
AI for Scientific Discovery
To be continued…